
Paris-Saclay University
About
I am a condensed matter theorist in the Theory group of LPS Orsay. My main research interests are symmetry-protected topological and strongly-interacting fractionalized phases in insulators and superconductors, the interplay of charge ordering and superconductivity, and the ways to probe all these phenomena experimentally using various lattice and electronic defects. Of special interest to me are two dimensional heterostructures, Dirac materials, and cuprate high-temperature superconductors.
In terms of methods, I enjoy both analytics and numerics.
Interests
- Topological matter and symmetry, classification
- Bound states and anyons, defects
- Charge and pair density waves, cuprates
- Dirac equation, graphene and TMDs
Education
- Undergraduate studies at the Department of Theoretical Physics, Faculty of Physics, University of Belgrade, with diploma thesis (2006) in the group of Prof. Milan Damnjanović.
- PhD (2010) in the group of Prof. Jan Zaanen at Lorentz Institute, Leiden University.
Highlighted Research Topics
At a glance: Why are defects interesting?

Defects, i.e., atomic or nanoscale imperfections in the crystalline or in the electronic order, can seemingly only elicit a local response of the electrons, adding to an average scattering — but this is a pessimistic view! Optimistically, defects can play three important roles: (1) If the defect is topological, its local probing of the system reflects deeply the quantum order, and hence can even identify new states of matter (see image). When the quantum state is itself topological, by definition it is non-local in nature, but this reflects in the local response to a topological defect, which can bind exotic and exceptionally robust electronic state. This leads to the possibility of (2) Engineering fractional defect-bound excitations, for example Majorana fermions and anyons, which can be externally manipulated and patterned into superlattices to design new collective quantum states. Even in a non-topological system, (3) The local response to topological defects can reveal the interplay between multiple intertwined electronic order parameters, or even reveal fluctuating and competing ordering tendencies.
Charge ordering in cuprate high-temperature superconductors
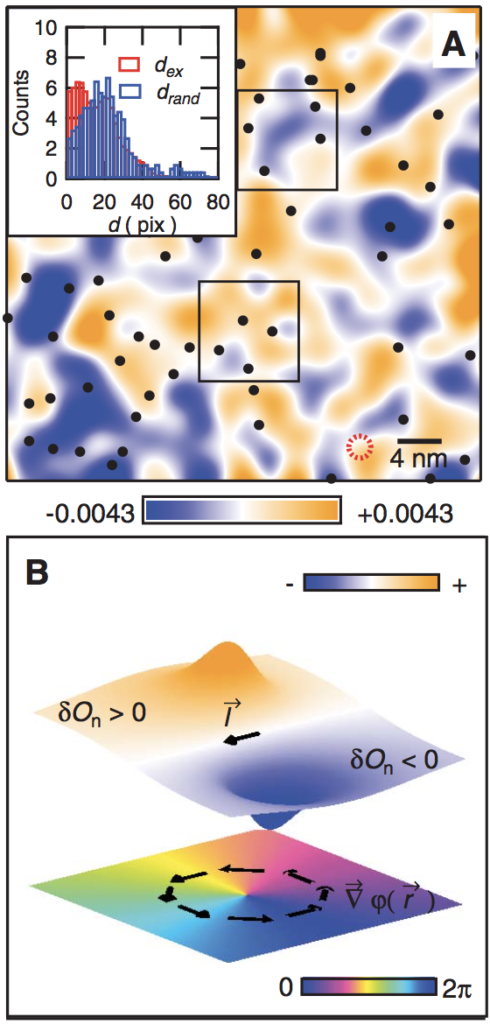
In cuprates, well-known high transition-temperature superconducting (HTC) materials, the physics of strong electron correlations leads to states in which electrons seem to break various symmetries by forming complex spatial patterns (reminiscent of “quantum liquid crystals”), i.e., there are charge density waves (think “smectic”), electronic orientational anisotropies (think “nematic”), and inhomogeneous superconducting pairing. These coexist and feed into the extraordinary HTC phenomena. I have been very lucky to work on disentangling some of these phenomena by studying Scanning Tunneling Spectroscopy (STS) data from the experimental group of Prof. J.C. Séamus Davis during my lasting collaboration at Cornell. In particular, (1) I worked on establishing the effective interplay of smectic and nematic orders thanks to identification of wave dislocations (image), (2) I utilized the subatomic precision of this STS to develop a more accurate method of extracting the period of the charge density wave, leading to a hypothesis of commensurate domains in underdoped cuprates, and (3) by precise modeling of the density waves I helped establish the first application of machine learning (neural networks) to STS data again leading to a non-trivial measurement of the wave parameters. I am lucky , and am very excited while exploring new collaborations on these topics in Orsay.
Textures in superconductors and Majorana bound states
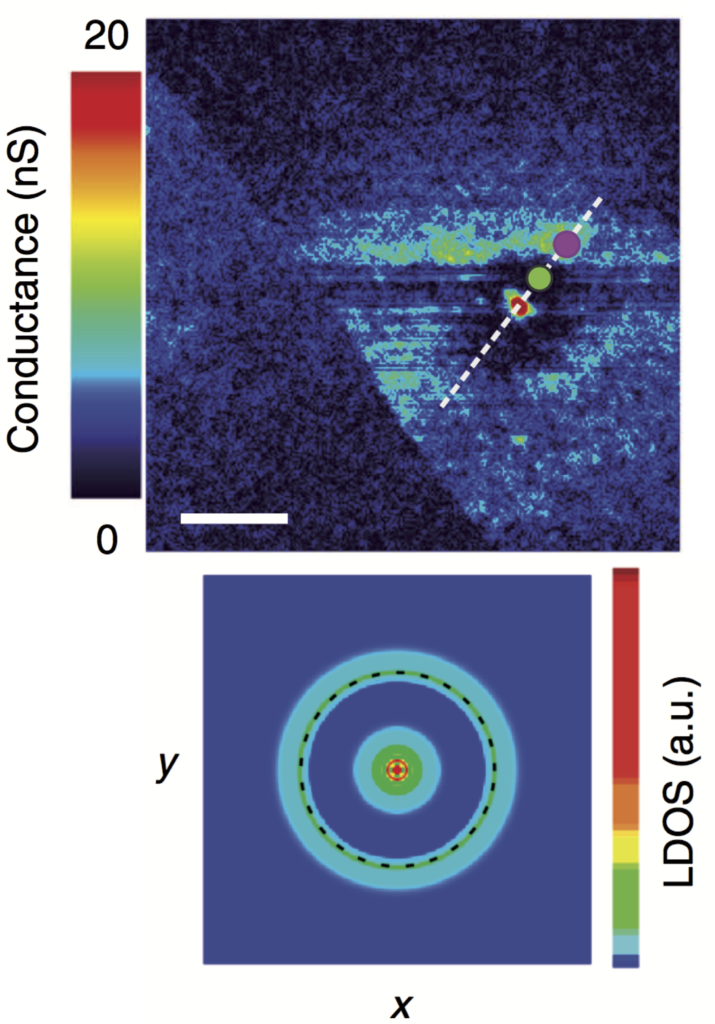
Topological superconductors (TSC) can host localized excitations called Majorana zero modes (MZM), whose manipulation could implement topological quantum computation. TSC require mixing superconductivity with magnetism and spin-orbit coupling in the same system, while MZM additionally require an inhomogeneity (e.g., an edge, a defect such as a superconducting vortex…) to bind them. Recently I worked on MZM in a two-dimensional superconductor, in contrast to the usual approach of making MZMs as endpoints of one-dimensional structures. With experimental collaborators at INSP-UPMC we identified a well-protected MZM bound by a vortex in spin-orbit coupling (image). We showed that this unusual vortex is related to a smooth texture in magnetic exchange field. Consequently we have predicted that topologically protected MZM appear in a superconductor without spin-orbit coupling, but proximitized by a magnetic skyrmion texture. Such proximitized heterostructures are now appearing in experiments. Relatedly, I have been also working on Shiba (not Majorana) bound states on magnetic impurities in superconductors, showing how their intricate spatial shape is a precise probe of the underlying Fermi surface and the superconducting pairing.
Topological band insulators, Dirac electrons and lattice defects
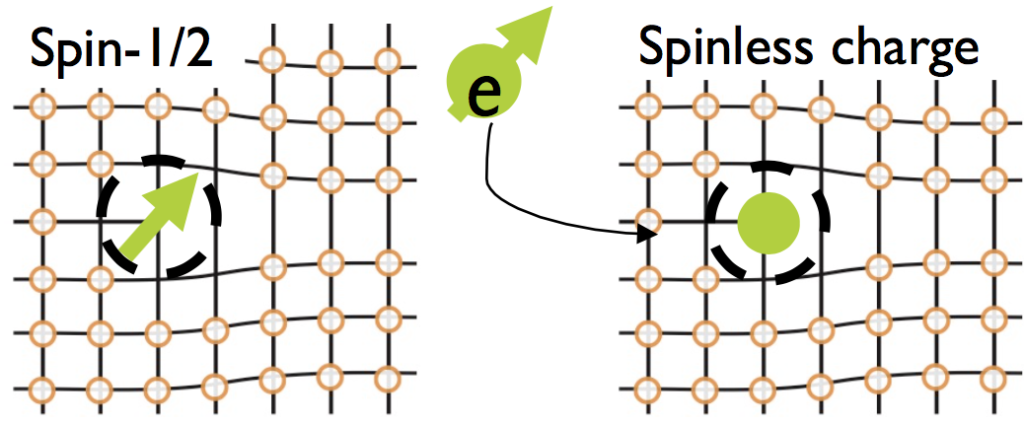
Various topological insulators (TI) are phases lacking true topological order, and hence are realizable in non-interacting systems. Then they are completely described by the topology of their bands, i.e., the topological numbers associated with wavefunctions as functions of momentum in the Brillouin zone. Crucially, the material’s local symmetries, lattice symmetries, and the considered number of bands determine which topological numbers are allowed and these remain protected as long as the energy gap between bands at the Fermi level doesn’t close. Such systems are realized in semiconductor crystals in both two- and three-dimensions. I am interested in how the topology protected by crystal symmetries can be experimentally accessed using topological crystal defects. Hence, after an elementary classification of so-called Crystalline TIs, I worked on extracting robust defect-bound anisotropic charge and spin fractionalization effects: the image is example in 2d, while in 3d protected one-dimensional electronic modes propagate (or do not) along the dislocation lines depending on the orientation of the defect line within the crystal. Although tight-binding numerics was necessary for these problems, a key complementary study was analytically with the low-energy continuum field theory. In bulk 2d TIs it is of mixed Dirac/Schroedinger type, while on the surface of 3d TIs it is a Dirac electron. This connects to my work on dislocations and grain boundaries in graphene, hosting Dirac electrons, and since more recently I am look at various defects in Transition Metal Dichalcogenides (TMDs), materials dubbed “graphene 2.0”, since beside the Dirac-like dispersion they have strong spin-orbit coupling and realize a variety of insulating, semiconducting, and superconducting phases. In these various Dirac-like theories topological defects tend to appear as singular gauge fields, so understanding the bound state solutions is directly connected to some universal and topological features in quantum field theory.
Topological orders with symmetry
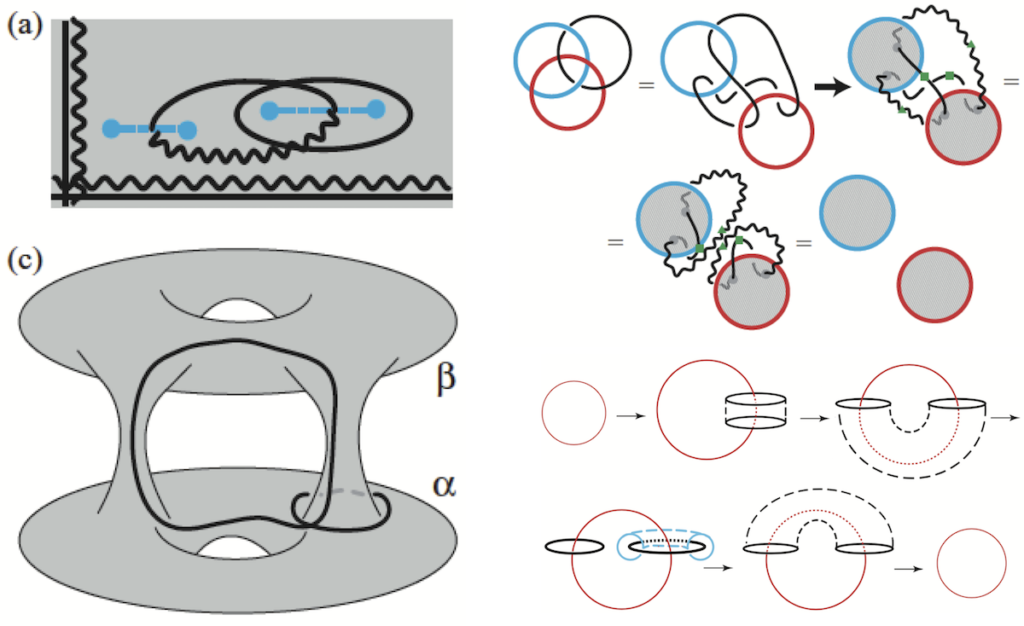
Topologically ordered (TO) phases of matter do not have any local symmetry-breaking order parameter, and can have intrinsic fractionalized quasiparticles (e.g., third of an electron charge in FQH systems), i.e., without necessity for external defects.
TO is a very distinct yet subtle property of the ground state, with the most basic feature that the degeneracy of the state depends on the topology of space itself, which seems a completely fixed parameter of life. Using external defects, however, we can effectively manipulate space itself. We considered multiple copies of an exactly solvable lattice model with TO, each model shifted in space. A dislocation defect of the entire lattice then non-trivially mixes the copies. Effectively, the defect merges multiple copies of our space into one space with non-trivial connectivity (image). In a 3d lattice the dislocation defect is itself a loop, and we considered knotted and linked dislocations loops, surprisingly such effects did not influence the resulting TO. Why does the topology of real space influence the ground state of TO system? The answer is that different ground states are related by having an intrinsic particle-anti-particle pair appear, tunnel across the entire system on a non-contractible path, and annihilate (tunneling paths are various black loops in the image). In fact all properties of TO are encoded in its quasiparticles, e.g., in the way they braid around each other in 2d. In 3d however there are both particle and loop excitations (here one sees an analogy between the gauge theories representing TO and the familiar electrodynamics gauge theory: in the latter, in 3d the excitations are charged particles and flux loops). To describe the TO in 3d the braiding of a point through a loop is obviously important, but not enough. A big surprise we found is that the other necessary ingredient to characterize TO in 3d is the simultaneous braiding of three loop excitations, not two (bottom right image). Finally, TO in presence of global symmetries is even richer with complex properties. We uncovered some degeneracies in the excitation spectrum of TO in arbitrary dimensions, coming from the presence of a global symmetry.
Theses
PhD thesis (Oct 2010) at Lorentz Institute, Leiden University, in the group of Prof. Jan Zaanen:
Dislocations in Stripes and Lattice Dirac Fermions
Selected
- Gerbold C Ménard, Andrej Mesaros, Christophe Brun, François Debontridder, Dimitri Roditchev, Pascal Simon, Tristan Cren,
Isolated pairs of Majorana zero modes in a disordered superconducting lead monolayer,
Nat Commun 10, 2587 (2019); (arXiv:1810.09541). - Mesaros A., Fujita K., Edkins S.D., Hamidian M.H., Eisaki H., Uchida S., J.C. Séamus Davis, Lawler M.J., Kim E.-A.,
Commensurate 4a0 period Charge Density Modulations throughout the Bi2Sr2CaCu2O8+x Pseudogap Regime,
PNAS 113, 12661 (2016); (arXiv:1608.06180). - Mesaros A. and Ran Y.,
A classification of symmetry enriched topological phases with exactly solvable models,
Phys. Rev. B 87, 155115 (2013); (arXiv:1212.0835). - Slager R.-J., Mesaros A., Juričić V. and Zaanen J.,
The space group classification of topological band insulators,
Nature Physics 9, 98 (2013); (arXiv:1209.2610). - Jiang S., Mesaros A. and Ran Y.,
Chiral spin-density wave, spin charge-Chern liquid, and d+id superconductivity in 1/4-doped correlated electronic systems on the honeycomb lattice,
Phys. Rev. X 4, 031040 (2014); (arXiv:1404.3452).
Papers
- Uldemolins M., Mesaros A. and Simon P.,
Quasiparticle focusing of bound states in two-dimensional s-wave superconductors,
Phys. Rev. B 105, 144503 (2022) ; (arXiv:2201.01750). - Touchais J.-B., Mesaros A. and Simon P.,
Robust propagating in-gap modes due to spin-orbit domain walls in graphene,
Phys. Rev. B 106, 035139 (2022); (arXiv:2107.10116). - Uldemolins M., Mesaros A. and Simon P.,
Effect of Van Hove singularities on Shiba states in two-dimensional -wave superconductors,
Phys. Rev. B 103, 214514 (2021); (arXiv:2104.03846).
- Garnier M., Mesaros A. and Simon P.,
Topological superconductivity with deformable magnetic skyrmions,
Commun Phys 2, 126 (2019); (arXiv:1904.03005). - Ménard G.C., Mesaros A., Brun C., Debontridder F., Roditchev D., Simon P. and Cren T.,
Isolated pairs of Majorana zero modes in a disordered superconducting lead monolayer,
Nat Commun 10, 2587 (2019); (arXiv:1810.09541). - Zhang Y.*, Mesaros A.*, Fujita K., Edkins S.D., Hamidian M.H., Ch’ng K., Eisaki H., Uchida S., J.C. Séamus Davis, Khatami E. and Kim E.-A.,
Machine Learning in Electronic Quantum Matter Imaging Experiments,
Nature 570, 484–490 (2019); (arXiv:1808.00479). - Mesaros A., Lawler M. J. and Kim E.-A.,
Nematic fluctuations balancing the zoo of phases in half-filled quantum Hall systems,
Physical Review B 95, 125127 (2017); (arXiv:1610.01171). - Mesaros A., Fujita K., Edkins S.D., Hamidian M.H., Eisaki H., Uchida S., J.C. Séamus Davis, Lawler M.J., Kim E.-A.,
Commensurate 4a0 period Charge Density Modulations throughout the Bi2Sr2CaCu2O8+x Pseudogap Regime,
PNAS 113, 12661 (2016); (arXiv:1608.06180). - Jiang S., Mesaros A. and Ran Y.,
Ferromagnetism and d+id superconductivity in 1/2-doped correlated systems on triangular lattice,
arXiv:1604.08615. - Jiang S., Mesaros A. and Ran Y.,
Chiral spin-density wave, spin charge-Chern liquid, and d+id superconductivity in 1/4-doped correlated electronic systems on the honeycomb lattice,
Physical Review X 4, 031040 (2014); (arXiv:1404.3452). - Jiang S., Mesaros A. and Ran Y.,
Generalized modular transformations in 3+1D topologically ordered phases and triple linking invariant of loop braiding,
Physical Review X 4, 031048 (2014); (arXiv:1404.1062). - Ye B., Mesaros A. and Ran Y.,
Possible high temperature odd parity superconductivity in LaNi7/8Co1/8O3 (111) bilayers,
Physical Review B 89, 201111(R) (2014); (arXiv:1402.6368). - Slager R.-J., Mesaros A., Juričić V. and Zaanen J.,
Interplay between electronic topology and crystal symmetry: Dislocation-line modes in topological band-insulators,
Physical Review B 90, 241403(R) (2014); (arXiv:1401.4044). - Mesaros A., Kim Y.-B. and Ran Y.,
Changing topology by topological defects in three-dimensional topologically ordered phases,
Physical Review B 88, 035141 (2013); (arXiv:1305.0214). - Mesaros A. and Ran Y.,
A classification of symmetry enriched topological phases with exactly solvable models,
Physical Review B 87, 155115 (2013); (arXiv:1212.0835). - Slager R.-J., Mesaros A., Juričić V. and Zaanen J.,
The space group classification of topological band insulators,
Nature Physics 9, 98 (2013); (arXiv:1209.2610). - Mesaros A., Slager R.-J., Zaanen J. and Juričić V.,
Zero-energy states bound to a magnetic pi-flux vortex in a two-dimensional topological insulator,
Nuclear Physics B 867, 977 (2012); (arXiv:1208.5708). - Juričić V., Mesaros A., Slager R.-J. and Zaanen J.,
Universal probes of two-dimensional topological insulators: dislocation and pi-flux,
Physical Review Letters 108, 106403 (2012); (arXiv:1108.3337). - Mesaros A., Fujita K., Eisaki H., Uchida S., Davis J. C., Sachdev S., Zaanen J., Lawler M. J. and Kim E.-A.,
Topological Defects Coupling Smectic Modulations to Intra-unit-cell Nematicity in Cuprates,
Science 333, 426 (2011); (arXiv:1108.0487). - Mesaros A., Papanikolaou S. and Zaanen J.,
Straining topological insulators as a way to detect Majorana fermions,
Physical Review B 84, 041409(R) (2011); (arXiv:1007.2350). - Mesaros A., Papanikolaou S., C.F.J. Flipse, Sadri D. and Zaanen J.,
Electronic States of Graphene Grain Boundaries,
Physical Review B 82, 205119 (2010); (arXiv:1007.1137). - Mesaros A., Sadri D. and Zaanen J.,
Parallel Transport in Graphene Parallels Gravity,
Physical Review B 82, 073405 (2010); (arXiv:0909.2703). - Mesaros A., Sadri D. and Zaanen J.,
Berry phase of dislocations in graphene and valley conserving decoherence,
Physical Review B 79, 155111 (2009); (arXiv:0811.1890). - Mukhin S. I., Mesaros A., Zaanen J. and Kusmartsev F. V.,
Enhanced electronic polarizability of metallic stripes and the universality of the bond-stretching phonon anomaly in high-temperature cuprate superconductors,
Physical Review B 76, 174521 (2007); (arXiv:0704.2622).
Quantum Theory of Condensed Matter — exercises (TD)
M2 QLMN at Paris-Saclay University: Sep 2022 – Dec 2022
Exercises (TD) at Master 2 level.
Notes (student access only)
Quantum Theory of Condensed Matter — exercises (TD)
M2 QLMN at Paris-Saclay University: Sep 2021 – Dec 2021
Exercises (TD) at Master 2 level.
Notes (student access only)
- A short CV (PDF)
Previous posts
- Postdoc (2017-2018) with Prof. Pascal Simon at LPS Orsay.
- Postdoc (2013-2017) with Prof. Eun-Ah Kim at LASSP of Cornell University.
- Postdoc (2010-2013) with Prof. Ying Ran at Department of Physics of Boston College.
- PhD (2006-2010) in the group of Prof. Jan Zaanen in the field of Condensed Matter Physics Theory.
Thesis: “Dislocations in Stripes and Lattice Dirac Fermions“
Seminar of the LPS Theory group
Since late 2018 I am the main organizer of the “Theory of Condensed Matter on the Plateau” seminar held since many years traditionally on Thursdays at 11h at LPS Orsay, and beginning with the Covid pandemic, in parallel on Zoom.
The calendar of upcoming talks and a short list of recent talks.
Contact me if you’d like to participate, or consider giving a talk.
Contact
- andrej.mesaros@universite-paris-saclay.fr
- +33 (0) 1 69 15 45 73
- Postal address: 1 rue Nicolas Appert, Bâtiment 510, 91405 Orsay Cedex, France
- How to reach LPS Orsay; Then, 1st floor, Aile Sud, office S104
You are always welcome to inquire about internships, and visit me in the Theory group of LPS Orsay, which is very collaborative.
My internship proposals are usually also advertised among others at LPS Orsay, on the ICFP Master page, and on the QLMN Master page.
Current internship proposals
PhD and Postdoc offers
PhD students
| Started | Subject | |
| Mateo ULDEMOLINS NIVELA | Sep 2020 | Impurities in unconventional superconductors (co-supervision with P. Simon and H. Aubin) |
| Jean-Baptiste TOUCHAIS | Sep 2019 | Topological states from inhomogeneous spin-orbit coupling (co-supervision with P. Simon) |
Interns
| Level | Semester | Subject | |
Previous PhD students
| Defended | Thesis | |
| Maxime GARNIER | Oct 2020 | Les textures magnétiques pour la supraconductivité topologique (co-supervised with P. Simon) |
Previous Interns
| Level | Semester | Subject | |
| Tangchao LIU | M1 | spring 2022 | Bound states in massive Dirac systems (co-supervised with P. Simon) |
| Mateo ULDEMOLINS NIVELA | M2 | spring 2020 | Exotic superconductivity in 2D Dirac materials (co-supervised with P. Simon) |
| Mateo ULDEMOLINS NIVELA | M1 | spring 2019 | Study of an inhomogeneous spin-orbit coupling in topological semiconducting wires (co-supervised with P. Simon) |
| Ramal AFROSE | M2 | summer 2019 | Topological states of SSH chain with spin-orbit coupling |
| J. J. Arfor HOUWMAN | M1 | spring 2019 | Majorana modes in s-wave superconductor proximitized skyrmions (co-supervised with P. Simon) |
| Jean-Baptiste TOUCHAIS | M2 | spring 2019 | Topological states from 2D inhomogeneous spin-orbit coupling (co-supervised with P. Simon) |
| Ana Marija NEDIĆ | M2 | spring 2017 | Localization and mixing of Majorana edge states (co-supervised with P. Simon) |
| Donald GOURY | M1 | spring 2017 | Stability of Majorana edge states in a topological superconductor (co-supervised with P. Simon) |