A magnetic domain wall moving in a magnetic film, a droplet sliding on a rough surface, a fracture propagating in a brittle material or a half-cooked spaghetti moving on a tilted sheet of abrasive paper… are a priori very different phenomena which present similar aspects.
All of them can be described by the motion of an elastic interface in the presence of defects which form a landscape of random pinning potential (see the inset in the figure). Each defect constitutes a small energy barrier which prevents the free motion of the interface but which can be overcome thanks to thermal activation. As the interfaces are elastic, they are collectively pinned by the defects and their form does not follow exactly the wells of the pinning potential.
The mechanisms of interface motion strongly depend on the strength of the driving force. For a small force, the interfaces are very sensitive to defects: the motion takes place by successive jumps over pinning barriers, and is named the creep motion. An increase of the force reduces the sensibility to defects and thus the effective height of pinning barriers. Beyond a threshold called the depinning force, the pinning barriers collapse and the interfaces are released from the defects. The creep motion close to a zero force and the depinning phenomenon just above the threshold are relatively well understood. Theories and experiments show that those phenomena are universal, that is, independent of the nature of studied system. On the other hand, for the whole range of force between these two limits, the universal or non-universal nature of the dynamic regimes stayed until now an open question.
In order to address this question, we have studied the motion of magnetic domains in various magnetic materials and over a wide temperature range. In this physical system, the force corresponds to the applied field and the elastic interface is the magnetic domain wall. We have shown that all the variations of domain wall velocity with applied field collapse on a unique master curve (see figure). This curve represents the reduced height of the pinning barrier as a function of the reduced force. It highlights the universal character of the whole creep regime up to the depinning force. Our results are also in good agreement with numerical simulations describing the motion of an elastic line in a disordered two dimensional medium.
As these simulations do not take into account specific properties of magnetic materials, our analysis is very probably relevant to understand the dynamics of interfaces in other systems physical as those enumerated at the beginning. On the other hand, our results should be particularly important for potential applications such as magnetic memories based on the controlled displacement of magnetic domain walls.
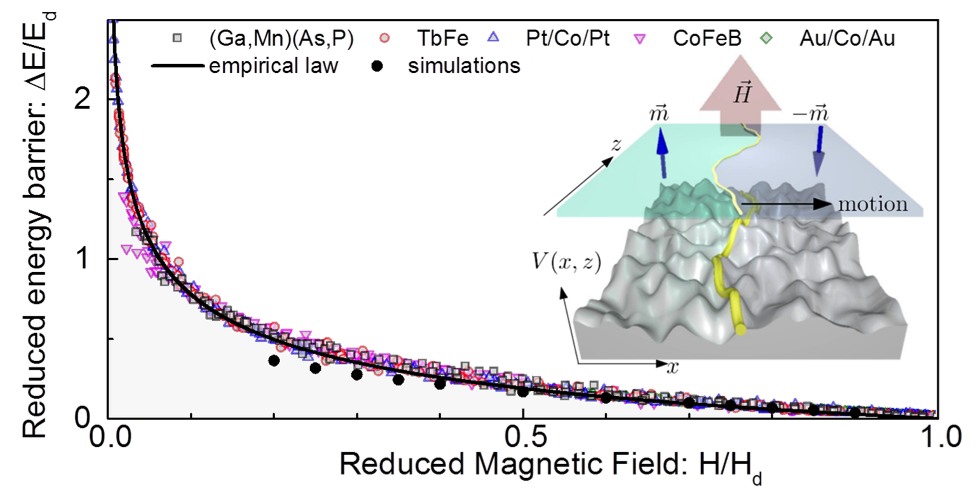
Curve. The variation of the reduced energy barrier height ∆E/Ed is reported as a function of the reduced force H/Hd, for five different magnetic materials and for temperature ranging from 10 to 315 Kelvin (25 curves are superimposed). This master curve shows the whole creep motion presents a universal character.