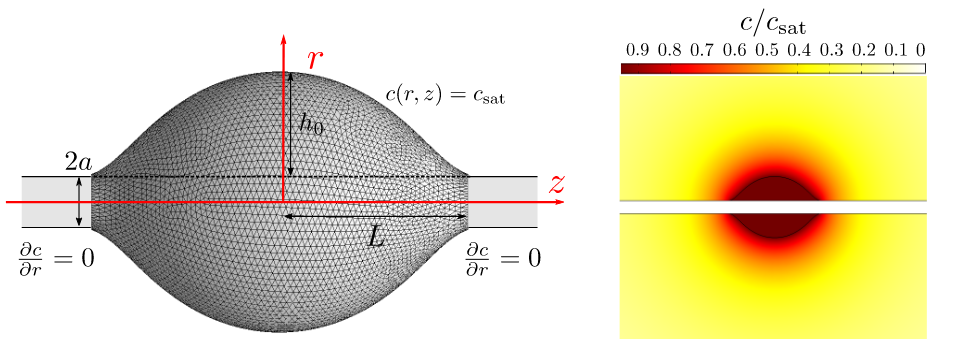
We investigate theoretically and numerically the diffusion-limited evaporation of a liquid deposited on a fiber in two configurations: a sleeve and a axisymmetric barrel-shaped droplet. For a sleeve, the local flux depends on both the aspect ratio and the smallest length of the problem. By using analytical calculations and 3D finite elements simulations, we predict a divergence of this flux further localized at the edge as the aspect ratio increases. The evaporation of axisymmetric drops on a fiber is studied with numerical simulations. We evidence that the evaporation rate is almost independent of the wetting properties of the liquid, even for small contact angles, and that the droplets evaporate as spheres of the same volume.
This paper, in collaboration with Julien Dervaux at MSC in Paris-Diderot university, is published in Europhysics Letters and is visible on arxiv.
